Geometry Matching

Geometry matching is the process of matching inferences to ground truths for computer vision workflows with a localization component, such as 2D and 3D object detection and instance segmentation. It is a building block for metrics like TP / FP / FN counts and any metrics derived from these, such as precision and recall.

While it may sound simple, geometry matching is surprisingly challenging and full of edge cases! In this guide, we'll focus on 2D object detection—specifically 2D bounding box matching—to learn about geometry matching algorithms.

• API Reference: match_inferences, match_inferences_multiclass ↗

Algorithm Overview

In a geometry matching algorithm, the following criteria must be met for a valid match:

1. The IoU between the inference and ground truth must be greater than or equal to a threshold
2. For multiclass workflows, inference label must match the ground truth label

Pseudocode: Geometry Matching

1. Loop through all images in your dataset;
2. Loop through all labels;
3. Get inferences and ground truths with the current label;
4. Sort inferences by descending confidence score;
5. Check against all ground truths and find a ground truth that results in maximum IoU;
6. Check for the following criteria for a valid match:
   1. This ground truth is not matched yet AND
   2. The IoU is greater than or equal to the IoU threshold;
7. Repeat 5-6 on the next inference;

Examples: Matching 2D Bounding Boxes

Let's apply the algorithm above to the following examples of 2D object detection. Bounding boxes (see: BoundingBox) in the diagrams below use the following colors based on their type and the matching result:

This example contains two ground truth and two inference bounding boxes, each with the same label. The pair \((\text{A}, \text{a})\) has high overlap (IoU of 0.9) and the pair \((\text{B}, \text{b})\) has low overlap (IoU of 0.13). Let's find out what the matched results look like in this example with a IoU threshold of 0.5:

Bounding Box	Score	IoU(\(\text{A}\))	IoU(\(\text{B}\))
\(\text{a}\)	0.98	0.9	0.0
\(\text{b}\)	0.6	0.0	0.13

Because inference \(\text{a}\) has a higher confidence score than inference \(\text{b}\), it gets matched first. It is pretty clear that ground truth \(\text{A}\) scores the highest IoU with inference \(\text{a}\), and IoU is greater than IoU threshold, so \(\text{a}\) and \(\text{A}\) are matched.

Next, inference \(\text{b}\) gets compared against all ground truth bounding boxes. Once again, it is clear that ground truth \(\text{B}\) scores the maximum IoU with inference \(\text{b}\), but this time IoU is less than the IoU threshold, so \(\text{b}\) becomes an unmatched inference.

Now that we have checked all inferences, any ground truth bounding boxes that are not matched yet are marked as unmatched. In this case, ground truth \(\text{B}\) is the only unmatched ground truth.

Bounding Box(es)	Match Type
\((\text{A}, \text{a})\)	Matched Pair
\(\text{B}\)	Unmatched Ground Truth
\(\text{b}\)	Unmatched Inference

Let's take a look at another example with multiple classes, Apple and Banana:

Bounding Box	Class	Score	IoU(\(\text{A}\))
\(\text{A}\)	Apple	—	—
\(\text{a}\)	Apple	0.3	0.0
\(\text{b}\)	Banana	0.5	0.8

Each class is evaluated independently. Starting with Apple, there is one ground truth \(\text{A}\) and one inference \(\text{a}\), but these two do not overlap at all (IoU of 0.0). Because IoU is less than the IoU threshold, there is no match for class Apple.

For class Banana, there is only one inference and no ground truths. Therefore, there is also no match for class Banana.

Bounding Box(es)	Match Type
\(\text{A}\)	Unmatched Ground Truth
\(\text{a}\)	Unmatched Inference
\(\text{b}\)	Unmatched Inference

Here is another example with multiple inferences overlapping with the same ground truth:

Bounding Box	Score	IoU(\(\text{A}\))
\(\text{a}\)	0.5	0.8
\(\text{b}\)	0.8	0.5

Among the two inferences \(\text{a}\) and \(\text{b}\), \(\text{b}\) has a higher confidence score, so \(\text{b}\) gets matched first. IoU between ground truth \(\text{A}\) and \(\text{b}\) is greater than the IoU threshold, so they become a match.

Inference \(\text{a}\) is compared with ground truth \(\text{A}\), but even though IoU is greater than the IoU threshold, they cannot become a match because \(\text{A}\) is already matched with \(\text{b}\), so inference \(\text{a}\) remains unmatched.

Bounding Box(es)	Match Type
\((\text{A}, \text{b})\)	Matched Pair
\(\text{a}\)	Unmatched Inference

Finally, let's consider another scenario where there are multiple ground truths overlapping with the same inference:

Bounding Box	Score	IoU(\(\text{A}\))	IoU(\(\text{B}\))
\(\text{a}\)	0.8	0.6	0.9

Inference \(\text{a}\) has a higher IoU with ground truth \(\text{B}\), so \(\text{a}\) and \(\text{B}\) become matched.

Bounding Box(es)	Match Type
\((\text{B}, \text{a})\)	Matched Pair
\(\text{A}\)	Unmatched Ground Truth

Comparison of Matching Algorithms from Popular Benchmarks

Geometry matching is a fundamental part of evaluation for workflows with localization. Metrics such as precision, recall, and average precision are built on top of these matches. The matching algorithm we've covered above is standard across various popular object detection benchmarks.

In this section, we'll examine the differences in matching algorithm from a few popular benchmarks:

• PASCAL VOC 2012
• COCO
• Open Images V7

PASCAL VOC 2012

The PASCAL VOC 2012 benchmark includes a difficult boolean annotation for each ground truth, used to differentiate objects that are difficult to recognize from an image. Any ground truth with the difficult flag and any inferences that are matched with a difficult ground truth will be ignored in the matching process. In other words, these ground truths and the inferences that are matched with them are excluded in the matched results. Hence, models will not be penalized for failing to detect these difficult objects, nor rewarded for detecting them.

Another difference that is noteworthy is how PASCAL VOC outlines the IoU criteria for a valid match. According to the evaluation section (4.4) in development kit doc, IoU must exceed the IoU threshold to be considered as a valid match.

Pseudocode: PASCAL VOC Matching

1. Loop through all images in your dataset;
2. Loop through all labels;
3. Get inferences and ground truths with the evaluating label;
4. Sort inferences by descending confidence score;
5. Check against all ground truths and find a ground truth that results in maximum IoU;
6. Check for the following criteria for a valid match:
   1. This ground truth is not matched yet AND
   2. The IoU is greater than the IoU threshold;
7. If matched with a difficult ground truth, ignore;
8. Repeat 5-7 on the next inference;

COCO

COCO (Common Objects in Context) labels its ground truth annotations with an iscrowd field to specify when a ground truth includes multiple objects. Similarly to how difficult ground truths are treated in PASCAL VOC, any inferences matched with these iscrowd ground truths, are excluded from the matched results. This iscrowd flag is intended to avoid penalizing models for failing to detect objects in a crowded scene.

Pseudocode: COCO Matching

1. Loop through all images in your dataset;
2. Loop through all labels;
3. Get inferences and ground truths with the evaluating label;
4. Sort inferences by descending confidence score;
5. Check against all ground truths and find a ground truth that results in maximum IoU;
6. Check for the following criteria for a valid match:
   1. This ground truth is not matched yet AND
   2. The IoU is greater than or equal to the IoU threshold;
7. If matched with a iscrowd ground truth, ignore;
8. Repeat 5-7 on the next inference;

Open Images V7

The Open Images V7 Challenge evaluation introduces two key differences in its matching algorithm.

The first is with the way that the images are annotated in this dataset. Images are annotated with positive image-level labels, indicating certain object classes are present, and with negative image-level labels, indicating certain classes are absent. Therefore, for fair evaluation, all unannotated classes are excluded from evaluation in that image, so if an inference has a class label that is unannotated on that image, this inference is excluded in the matching results.

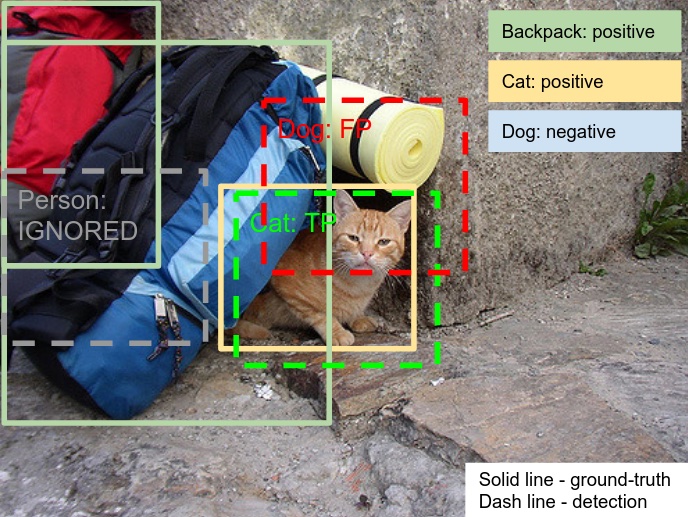
An example of non-exhaustive image-level labeling from Open Images V7

The second difference is with handling group-of boxes, which is similar to iscrowd annotation from COCO but is not just simply ignored. If at least one inference is inside the group-of box, then it is considered to be a match. Otherwise, the group-of box is considered as an unmatched ground truth. Also, multiple correct inferences inside the same group-of box still count as a single match:

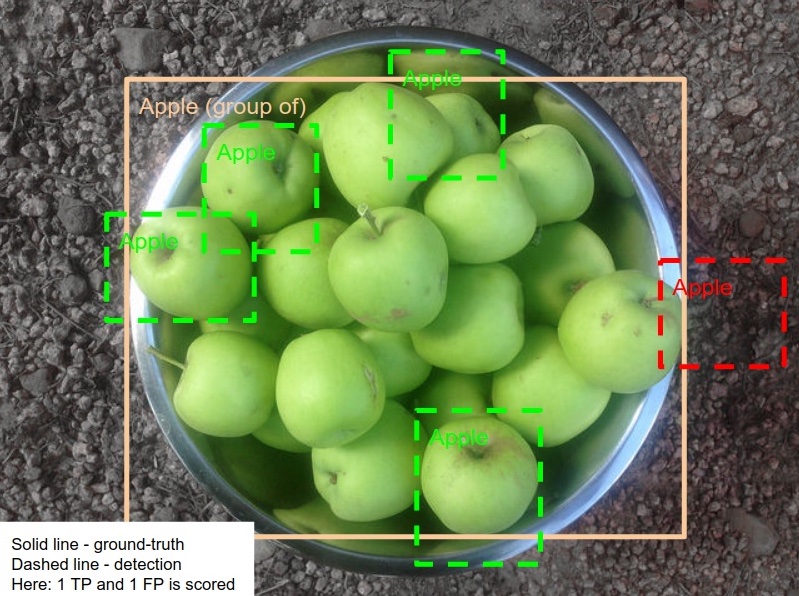
An example of group-of boxes from Open Images V7

Pseudocode: Open Images V7 Matching

1. Loop through all images in your dataset;
2. Loop through all positive image-level labels;
3. Get inferences and ground truths with the evaluating label;
4. Sort inferences by descending confidence score;
5. Check against all non-ground-of ground truths and find a ground truth that results in maximum IoU;
6. Check for the following criteria for a valid match:
   1. This ground truth is not matched yet AND
   2. The IoU is greater than or equal to the IoU threshold;
7. If matched with a difficult ground truth, ignore;
8. Repeat 5-7 on the next inference;
9. Loop through all unmatched inferences;
10. Check against all group-of ground truths and find a ground truth that results in maximum IoU;
11. Check for the matching criteria (6);
12. Repeat 10-11 on the next unmatched inference;

Limitations and Biases

The standard matching algorithm appears to have an undesirable behavior when there are many overlapping ground truths and inferences with high confidence scores due to its greedy matching. Because it optimizes for higher confidence score and maximum IoU, it can potentially miss valid matches by matching a non-optimal pair, resulting in a poorer matching performance.

Example: Greedy Matching

Bounding Box	Score	IoU(\(\text{A}\))	IoU(\(\text{B}\))
\(\text{a}\)	0.7	0.0	0.6
\(\text{b}\)	0.8	0.5	0.7

When there are two ground truths and two inferences, one inference \(\text{b}\) with a higher score overlaps well with both ground truths \(\text{A}\) and \(\text{B}\), and the other one, \(\text{a}\), with a lower score overlaps well with just one ground truth \(\text{B}\). Because the IoU between \(\text{B}\) and \(\text{b}\) is greater than IoU between \(\text{A}\) and \(\text{b}\), inference \(\text{b}\) is matched with ground truth \(\text{B}\), causing inference \(\text{a}\) to fail to match.

This greedy matching behavior results in a higher false positive count in this type of scenario. Ideally, inference \(\text{a}\) matches with ground truth \(\text{B}\), and inference \(\text{b}\) matches with ground truth \(\text{A}\), resulting in no FPs.

Another behavior to note here is that it is possible to get different matching results depending on the ground truth order when there are multiple ground truths overlapping with an inference with the equal IoU or depending on the inference order when there are multiple inferences overlapping with a ground truth with the equal confidence score.

Example: Different Matching Results When Ground Truth Order Changes

Bounding Box	Score	IoU(\(\text{A}\))	IoU(\(\text{B}\))
\(\text{a}\)	0.7	0.0	0.5
\(\text{b}\)	0.7	0.5	0.5

The three pairs of ground truth and inference have same IoU and both inferences have same confidence score.

If the ground truths are ordered as \([\text{A}, \text{B}]\) and the inferences as \([\text{a}, \text{b}]\), inference \(\text{a}\) is matched with \(\text{B}\) first, so inference \(\text{b}\) gets matched with \(\text{A}\).

If the inference order changes to \([\text{b}, \text{a}]\), now inference \(\text{a}\) may or may not be matched with any ground truth. The matched result can change depending on the ground truth order. If \(\text{A}\) is evaluated before \(\text{B}\), inference \(\text{b}\) is matched with \(\text{A}\), and \(\text{a}\) can be matched with \(\text{B}\). However, if \(\text{B}\) comes before \(\text{A}\), inference \(\text{b}\) is matched with \(\text{B}\) instead, leaving inference \(\text{a}\) with no match.

As discussed earlier, the standard matching algorithm compares model inferences with annotated ground truths in two fundamental aspects: localization and classification. The comparison generates results, which entail matched pairs, unmatched ground truths, and unmatched inferences; however, these results do not reveal why certain matches were unsuccessful. A myriad of reasons can lead to a failed match, such as poor localization due to insufficient overlap (IoU), or good localization but poor classification. Surfacing these types of errors is profoundly useful during model debugging. For instance, confused matches where localization succeeded (i.e. IoU above the IoU threshold) but classification failed (i.e. mismatching label values) can be identified by matching unmatched inferences with unmatched ground truths once more after the initial matching. Confused matches are useful for creating a confusion matrix to focus on a detection model's classification performance.